Gamma 分布表达式:别怕,它没那么可怕!
嘿,小伙伴们!今天咱们来聊聊 Gamma 分布表达式,也就是 Gamma 分布的概率密度函数。别看它名字很唬人,其实它没那么可怕,就像……嗯,就像我一样,看起来很厉害,其实内心住着一个小可爱!
Gamma 分布,一个神奇的家伙
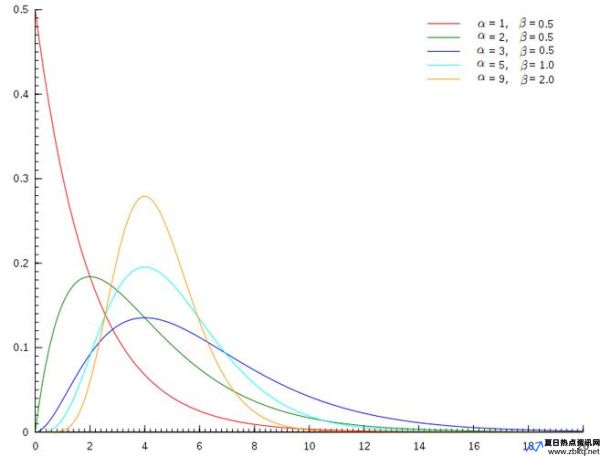
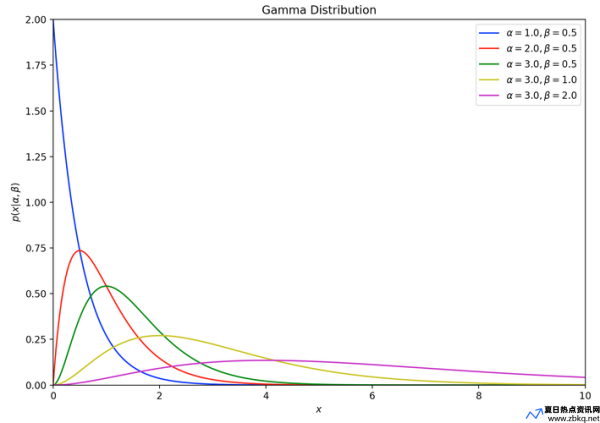
Gamma 分布,它可是统计学中一个相当重要的分布,经常用来描述各种各样的事件,比如:
等待时间: 你在公交车站等车,等了多久才来?
设备寿命: 你新买的手机,能用多久?
事件发生次数: 一天之内,你收到多少条微信?
这些都可以用 Gamma 分布来描述,因为它可以用来描述非负连续随机变量的概率分布,也就是那些只能取正数且可以取任意小数的随机变量。
Gamma 分布的表达式:别怕,我给你解释!
Gamma 分布的表达式,其实就是它的概率密度函数,长得有点像这样:
f(x; α, β) = (1 / (β^α Γ(α))) x^(α-1) e^(-x/β)
别被这个公式吓到!我们来拆解一下:
x: 表示我们要研究的随机变量,比如等待时间、设备寿命等等。
α: 被称为形状参数, 它决定了 Gamma 分布的形状,就像一个人的身高,决定了你的体型一样。
β: 被称为尺度参数, 它决定了 Gamma 分布的尺度,就像一个人的体重,决定了你胖瘦一样。
Γ(α): 被称为伽玛函数, 是一个特殊的函数,用来计算 Gamma 分布的归一化常数,确保概率密度函数的积分等于 1。
表格来帮忙!
为了让你更直观地理解 Gamma 分布表达式,我特意准备了一个方便你快速找到你要找的信息:
| 参数 | 解释 | 影响 |
|---|---|---|
| x | 随机变量 | 决定了 Gamma 分布的取值范围 |
| α | 形状参数 | 决定了 Gamma 分布的形状 |
| β | 尺度参数 | 决定了 Gamma 分布的尺度 |
| Γ(α) | 伽玛函数 | 确保概率密度函数的积分等于 1 |
几个常见的 Gamma 分布
根据参数的不同,Gamma 分布可以呈现出不同的形状:
α = 1, β = 1: 此时 Gamma 分布退化为指数分布,描述了事件发生的等待时间。
α > 1: 此时 Gamma 分布呈现出右偏的形状,描述了事件发生的次数或设备的寿命。
α < 1: 此时 Gamma 分布呈现出左偏的形状,描述了事件发生的次数或设备的寿命。
Gamma 分布的应用:它可厉害了!
Gamma 分布在很多领域都有着广泛的应用,比如:
可靠性分析: 预测产品寿命和可靠性。
风险管理: 评估风险发生的概率和影响。
机器学习: 构建模型和进行预测。
想问问你:
你对 Gamma 分布有什么看法呢?你觉得它难吗?你觉得它有用吗?欢迎留言告诉我你的想法!
记住,数学并不枯燥,只要我们用心去理解,就会发现它的美丽和神奇!